Persamaan Lingkaran
Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak sama terhadap suatu titik tertentu. Titik tertentu itu disebut pusat lingkaran, sedangkan jarak titik terhadap pusat lingkaran disebut jari-jari lingkaran.
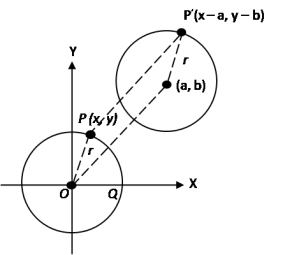
Gambar dibawah ini menunjukkan lingkaran dengan pusat P dan jari-jari r.
1. Persamaan lingkaran yang berpusat O (0, 0) dan jari-jari r
Pada lingkaran disamping jari-jari atau r = OP, OQ = x dan PQ = y.
Jarak dari O (0, 0) ke P (x, y) adalah.
Berdasarkan rumus Pythagoras
Jadi persamaan lingkaran dengan pusat O (0, 0) dan jari-jari r adalah x2 + y2 = r2
Contoh :
Tentukan persamaan lingkaran yang berpusat O (0, 0) dan jari-jari 5
Jawab :
2. Persamaan lingkaran yang berpusat P (a, b) dan berjari-jari r
Persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r dapat diperoleh dari persamaan lingkaran yang berpusat di (0, 0) dan berjari-jari r dengan menggunakan teori pergeseran. Jika pusat (0, 0) bergeser (a, b) maka titik (x, y) bergeser ke (x + a, y + b).
Kita peroleh persamaan.
Persamaan lingkaran menjadi (x’– a)2 + (y’ – b)2 = r2
Jadi persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah (x- a)2 + (y – b)2 = r2
Contoh 1 :
Tentukan persamaan lingkaran yang berpusat di (3, 2) dan berjari-jari 4
Jawab :
Pusat (3, 2) maka a = 3 dan b = 2
Persamaan lingkaran (x- a)2 + (y – b)2 = r2
(x- 3)2 + (y – 2)2 = 42
(x- 3)2 + (y – 2)2 = 16
Contoh 2 :
Tentukan persamaan lingkaran berpusat di titik P(2, 3) yang melalui Q(5, -1)
Jawab :
Pusat (2, 3) maka a = 2 dan b = 3
Persamaan lingkaran (x- a)2 + (y – b)2 = r2
(x- 2)2 + (y – 3)2 = 252
B. Bentuk umum persamaan lingkaran
Persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah
(x- a)2 + (y – b)2 = r2
x2 – 2ax + a2 + y2 – 2by + b2 = r2
x2+ y2 – 2ax – 2by + a2+ b2– r2 = 0 atau x2+ y2 + Ax + By + a2+ b2+ C= 0
Jadi bentuk umum persamaan lingkaran x2+ y2 + Ax + By + a2+ b2+ C= 0
Contoh :
Tentukan pusat dan jari-jari lingkaran x2+ y2 – 4x +2y – 20= 0
Jawab :
A = -4, B = 2, dan C = -20
B. Kedudukan Titik dan Garis Pada Lingkaran
Kedudukan Titik Pada Lingkaran
Kedudukan Garis Pada Lingkaran
Untuk mengetahui kedudukan/ posisi sebuah garis terhadap lingkaran, substitusikan garis terhadap lingkaran sehingga didapatkan bentuk ax2+bx+c=0.
Letak K (m,n) terhadap X2+Y2 +Ax + By +C= 0 , ditentukan oleh nilai kuasa titik tersebut terhadap lingkaran
nilai kuasa K = m2+n2 +Am + Bn +C,
nilai kuasa K = m2+n2 +Am + Bn +C,
- K < 0
 di dalam lingkaran
di dalam lingkaran - K= 0
 pada lingkaran
pada lingkaran - K > 0
 di luar lingkaran
di luar lingkaran
Contoh 1:
Tentukan kedudukan titik-titik berikut terhadap lingkaran X2+y2 -8x -10y +16 =0 dan gambarlah
a. H(-3,9) b L(7,9), c M(10,5), d N(1,7)
Jawaban:Tentukan kedudukan titik-titik berikut terhadap lingkaran X2+y2 -8x -10y +16 =0 dan gambarlah
a. H(-3,9) b L(7,9), c M(10,5), d N(1,7)
- H(-3,9)
 K = (-3)2+92 -8.(-3) -10.9 +16 = 40, K > 0, diluar lingkaran
K = (-3)2+92 -8.(-3) -10.9 +16 = 40, K > 0, diluar lingkaran - L(7,9)
 K = (7)2+92 -8.(7) -10.9 +16 = 0, K = 0, pada lingkaran
K = (7)2+92 -8.(7) -10.9 +16 = 0, K = 0, pada lingkaran - M(10,5) K = (10)2+52 -8.(10) -10.5 +16 = 11, K > 0, diluar lingkaran
- N(1,7) K = 12+72 -8.(1) -10.7 +16 = -12, K < 0, didalam lingkaran
Contoh 2:
Diketahui sebuah lingkaran X2+y2 -2x +6y -15 =0 dan sebuah titik S(m,1), tentukan batas nilai m agar
Diketahui sebuah lingkaran X2+y2 -2x +6y -15 =0 dan sebuah titik S(m,1), tentukan batas nilai m agar
- titik S didalam lingkaran
- titik S diluar lingkaran
| S(m,1) | = kuasa |
| = m2 +12 - 2m +6.1 - 15 | |
| = m2 - 2m - 8 |
| a. | Syarat di dalam lingkaran, K< 0 m2 -2m -8 <0 (m-4)(m+2)=0 |
| m=-2 atau m=4 | |
| didalam lingkaran jika -2 < m <4 ( daerah - - - ) | |
| diluar lingkran, K >0, jika m<-2 atau m >4 (daerah ++ ) |
Kedudukan Garis Pada Lingkaran
Untuk mengetahui kedudukan/ posisi sebuah garis terhadap lingkaran, substitusikan garis terhadap lingkaran sehingga didapatkan bentuk ax2+bx+c=0.
Lihat diskriminannya: 

Jika
- D<0, berarti garis berada di luar lingkaran (tidak memotong lingkaran)
- D=0, berarti garis menyinggung lingkaran
- D>0, berarti garis memotong lingkaran di 2 titik berbeda.
Contoh 1:
- Tentukan posisi garis:
 terhadap lingkaran
terhadap lingkaran 
Jawab:
Karena 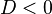 , maka garis berada di luar lingkaran.
, maka garis berada di luar lingkaran.
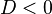 , maka garis berada di luar lingkaran.
, maka garis berada di luar lingkaran.
Contoh 2:
- Tentukan p agar garis
 terletak di luar lingkaran
terletak di luar lingkaran 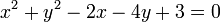 !
!
Jawab:
- syarat:
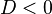
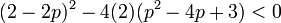



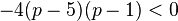
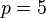 atau
atau 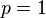
Gambar dengan garis bilangan untuk pertidaksamaan diatas, maka akan didapatkan nilai p:  atau
atau 
 atau
atau 
C. Persamaan Garis Singgung Lingkaran
Jika persamaan lingkaran 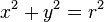 , maka persamaan garis singgungnya:Persamaan garis singgung untuk suatu titik (x1,y1) yang terletak pada lingkaran
, maka persamaan garis singgungnya:Persamaan garis singgung untuk suatu titik (x1,y1) yang terletak pada lingkaran
- Jika persamaan lingkaran
 , maka persamaan garis singgungnya:
, maka persamaan garis singgungnya:
- Jika persamaan lingkaran berbentuk
 , maka persamaan garis singgungnya:
, maka persamaan garis singgungnya:
Persamaan lingkaran  dapat juga diubah menjadi
dapat juga diubah menjadi  dengan kuadrat sempurna, sehingga rumus yang harus dihafalkan jadi lebih sedikit.
dengan kuadrat sempurna, sehingga rumus yang harus dihafalkan jadi lebih sedikit.
 dapat juga diubah menjadi
dapat juga diubah menjadi  dengan kuadrat sempurna, sehingga rumus yang harus dihafalkan jadi lebih sedikit.
dengan kuadrat sempurna, sehingga rumus yang harus dihafalkan jadi lebih sedikit.
Rumus:
 atau
atau 
- Jika diketahui titik
- Jika diketahui gradien
- Contoh soal :
- Soal No. 1
Diberikan persamaan lingkaran:
L ≡ x2 + y2 = 25.
Tentukan persamaan garis singgung lingkaran yang memiliki titik singgung di (−4, 3).
Pembahasan
Menentukan garis singgung pada suatu lingkaran yang pusatnya di (0, 0) dan diketahui titik singgungnya.
Lingkaran L ≡ x2 + y2 = r2
Titik singgung (x1, y1)Persamaan garis singgungnya adalah:

Dengan x1 = − 4 dan y1 = 3, persamaan garisnya:
−4x + 3y = 25
3y −4x − 25 = 0
Soal No. 2
Persamaan garis singgung pada lingkaran x2 + y2 = 13 yang melalui titik (3, −2) adalah....
A. 2x − 3y = −13
B. 2x − 3y = 13
C. 3x − 2y = − 14
D. 3x − 2y = 13
E. 3x + 2y = 13
(Garis singgung lingkaran - uan 2002)
Pembahasan
Titik yang diberikan adalah (3, −2), dan belum diketahui posisinya pada lingkaran, apakah di dalam, di luar atau pada lingkaran. Cek terlebih dahulu,
(3, −2) → x2 + y2
= 32 + (−2)2 = 9 + 4
= 13
Hasilnya ternyata sama dengan 13 juga, jadi titik (3, −2) merupakan titik singgung. Seperti nomor 1:

Soal No. 3
Diberikan persamaan lingkaran L ≡ x2 + y2 = 25. Tentukan persamaan garis singgung pada lingkaran tersebut yang memiliki gradien sebesar 3.
Pembahasan
Menentukan persamaan garis singgung pada lingkaran yang pusatnya di (0, 0) dengan diketahui gradien garis singgungnya.

Soal No. 4
Salah satu persamaan garis singgung lingkaran x2 + y2 = 25 yang tegak lurus garis 2y − x + 3 = 0 adalah....
A. y = −1/2 x + 5/2√5
B. y = 1/2 x − 5/2√5
C. y = 2x − 5
D. y = −2x + 5√5
E. y = 2x + 5
(Garis singgung Lingkaran - un 2005)
Pembahasan
Garis 2y − x + 3 = 0 memiliki gradien sebesar 1/2. Garis lain yang tegak lurus dengan garis ini harus memiliki gradien − 2. Ingat pelajaran SMP 8, jika dua garis saling tegak lurus maka berlakum1 ⋅ m2 = − 1
Sehingga persamaan garis singgung di lingkaran x2 + y2 = 25 yang memiliki gradien −2 adalah:

Jadi persamaan garis singgungnya bisa y = −2x + 5√5 bisa juga y = −2x − 5√5, pilih yang ada.
Soal No. 5
Diberikan persamaan lingkaran:
L ≡ (x − 2)2 + (y + 3)2 = 25
Tentukan persamaan garis singgung lingkaran dengan titik singgung pada (5, 1).
Pembahasan
Persamaan garis singgung pada lingkaran:L ≡ (x − a)2 + (y − b)2 = r2pada titik singgung (x1, y1)

dengan
a = 2 dan b = −3 dan r2 = 25
maka persamaan garisnya
 Soal No. 6
Soal No. 6
Diberikan persamaan lingkaran:
L ≡ (x − 2)2 + (y + 3)2 = 25
Tentukan persamaan garis singgung pada lingkaran tersebut yang sejajar dengan garis y = 2x + 3.
Pembahasan
Garis singgung pada lingkaran dengan pusat (a, b) diketahui gradien m

Garis singgung yang diminta sejajar dengan garis y = 2x + 3 sehingga gradiennya sama yaitu 2.

Soal No. 7
Persamaan garis singgung pada lingkaran x2 + y2 − 2x + 4y − 220 = 0 yang sejajar dengan garis 5 y + 12x + 8 = 0 adalah...
A. 12 x + 5y − 197 = 0 dan 12x + 5y + 195 = 0
B. 12 x + 5y + 197 = 0 dan 12x + 5y − 195 = 0
C. 5 x + 12y + 197 = 0 dan 5x + 12y + 195 = 0
D. 5x + 12y − 197 = 0 dan 5x + 12y − 195 = 0
E. 12 x − 5y − 197 = 0 dan 12x − 5y + 195 = 0
Pembahasan
Lingkaran x2 + y2 − 2x + 4y − 220 = 0 memiliki pusat:

dan jari-jari

Gradien garis singgungnya sejajar dengan 5 y + 12x + 8 = 0, jadi gradiennya adalah −12/5.
Persamaannya:

Sehingga dua buah garis singgungnya masing-masing adalah
 Soal No. 8
Soal No. 8
Persamaan garis singgung lingkaran x2 + y2 − 4x + 2y − 20 = 0 di titik (5, 3) adalah....
A. 3x − 4y + 27 = 0
B. 3x + 4y − 27 = 0
C. 3x + 4y − 27 = 0
D. 7x+ 4y − 17 = 0
E. 7x + 4y − 17 = 0
(UN 2005)
Pembahasan
Titik singgung : (x1, y1)
pada lingkaran : L ≡ x2 + y2 + Ax + By + C = 0
Rumus garis singgungnya:

Data:
x2 + y2 − 4x + 2y − 20 = 0
Titik (5, 3)
A = −4
B = 2
C = − 20
x1 = 5
y1 = 3
Garis singgungnya:

Soal No. 9
Persamaan garis singgung lingkaran x2 + y2 − 6x + 4y − 12 = 0 di titik (7, 1) adalah….
A. 3x − 4y − 41 = 0
B. 4x + 3y − 55 = 0
C. 4x − 5y − 53 = 0
D. 4x + 3y − 31 = 0
E. 4x − 3y − 40 = 0
(un 2011)
Pembahasan
Data soal:
L ≡ x2 + y2 − 6x + 4y − 12 = 0
A = −6
B = 4
C = − 12
(7, 1)
x1 = 7
y1 = 1
Rumus sebelumnya, diperoleh garis singgung lingkaran:

Soal No. 10
Lingkaran L ≡ (x + 1)2 + (y − 3)2 = 9 memotong garis y = 3. Garis singgung lingkaran yang melalui titik potong antara lingkaran dan garis tersebut adalah...
A. x = 2 dan x = − 4
B. x = 2 dan x = − 2
C. x = − 2 dan x = 4
D. x = − 2 dan x = − 4
E. x = 8 dan x = − 10
(Garis singgung lingkaran - un 2009 dan un 2012)
Pembahasan
Data soal:
Polanya:
L ≡ (x − a)2 + (y − b)2 = r2
Pusatnya (a, b)
L ≡ (x + 1)2 + (y − 3)2 = 9
a = −1
b = 3
y = 3 memotong lingkaran ini, masukkan nilai y ke persamaan, ketemu nilai x, dengan demikian titik-titik singgungnya akan diketahui.
(x + 1)2 + (y − 3)2 = 9
(x + 1)2 + (3 − 3)2 = 9
(x + 1)2 + 0 = 9
(x + 1)2 = 9
(x + 1) = ±3x + 1 = 3
x = 2x + 1 = −3
x = −4
Titik singgungnya: ( −4, 3) dan (2, 3)

Untuk titik singgung (x1, y1) = ( −4, 3) dengan pusatnya tadi (a, b) = (−1, 3)

Untuk titik singgung (x1, y1) = ( 2, 3) dengan pusatnya tadi (a, b) = (−1, 3)



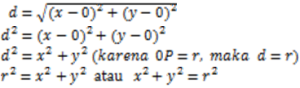
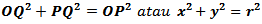
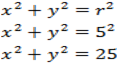
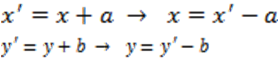
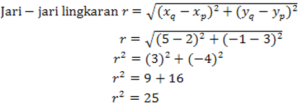
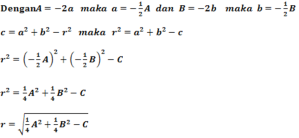

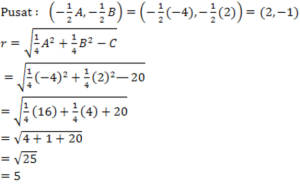
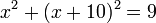



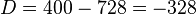
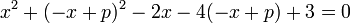
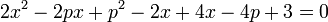


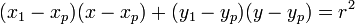

izin di copas ya buat bahan ppt :) terimakasihh
ReplyDeletemakasih kak ilmunya
ReplyDeletegan gambar nya ilang yg titik terhadap lingkaran, tolong baikin(Reupl0ad) dong
ReplyDeleteokee makasih yaa
ReplyDeleteIzin copy ya :D
ReplyDeletemakasih kaka
Izin copy ya :D
ReplyDeletemakasih kaka
penyajiannya cukup bagus
ReplyDeleteTerima kasih, Sangat bermanfaat sekali..
ReplyDeletemantap jadi gampang ngerjaiinnya (y)
ReplyDeleteini materi bagus, terim kasih
ReplyDeleteini manfaat banget, buat tugas sekolah makasih
ReplyDeletekak saya mau nanya .untuk soal no.7 Persamaan garis singgung pada lingkaran x2 + y2 − 2x + 4y − 220 = 0 yang sejajar dengan garis 5 y + 12x + 8 = 0 adalah......... kalau misalkan itukan yang sejajar dengan garis kalau saling tegak lurus dengan garis
ReplyDeletegimana caranya ????
yang diatas yang sejajar makanya m2=m1. kalau itu yg saling tegak lurus, cari m2 nya, dengan rumus m1.m2 = -1.
DeleteIzin mau di copy yah, terimakasih..
ReplyDeleteTrimakasih ilmunya kak, izi copy ya
ReplyDeleteKa kalo soalnya gini gimana?
ReplyDeleteHitunglah A,B, dan C. Jika lingkaran x2+y2+Ax+By+C=0 melalui (3,5), (-2,4), dan (-6,-2)
Bagus gan materinya... thanks..!!
ReplyDeletethanks ya kak for materi ini,, aku kebantu banget bikin bahan,, izin ambil sebagai daftar pustaka juga nih..
ReplyDelete#76
izin copy yaa buat tugas thx;)
ReplyDeleteMakasih Mas atas ilmunya
ReplyDeleteringkasan materinya bisa bantu tapi mungkin kurang kompelit dalam masalah soal serta pembahasannnya yang kurang menjurus atau mungkin kurang mendalam, tapi akasih ilmunya ;)
ReplyDeleteSangat membantu,terhindar dari ancaman guru killer,makasih mas
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteSaya mau tanya, saya masih ragu materi tentang garis singgung. no 4 kenapa diperoleh gradien= -2 ?
ReplyDeleteNo6 kenapa m=2.
Terus apa rumus untuk mencari gradien?
Terima kasih
trimaksih catatannya..
ReplyDeletesangat bermanfaat.
izin copy ya kak buat tugas ppt
ReplyDeleteIjin di copy ya..buat materi...
ReplyDeleteTerimakasih..
Makasih google
ReplyDeleteTerima kasih kak
ReplyDeleteitu kok gambar ny gk muncul muncul pas di rumus garis singgung
ReplyDeletejdinya binggung nihk
DeleteTerima kasih Kak, sangat membantu.. 👍
ReplyDeleteMantap kak👍
ReplyDeleteMantap kak👍
ReplyDeleteSaya masih bingung yang no 8 kok itu hasilnya 27=0? Kan -10-20 hasilnya -30 apa dpt dari yg lain? Maaf kalo salah
ReplyDeleteIzin copas buat materi presentasi
ReplyDeleteMakasih, kak
makasih kaa
ReplyDeleteizin kopas ya kak. terimakasih
ReplyDeleteizin copy paste kk,mksiih ilmunya
ReplyDeleteIzin copy paste ya kak, makasih juga buat ilmunya
ReplyDeleteMoh ferrynanda saputra
ReplyDeleteizin kopas ya kak... terima kasih
ReplyDeleteThe web site is lovingly serviced and saved as much as date. So it should be, thanks for sharing this with us 먹튀폴리스
ReplyDeletePenyajiannya bagus, mudah dipahami 😊
ReplyDelete