Statistika Matematika
Pelajaran Statistika di tingkat SMA meliputi mean, modus, median, jangkauan, simpangan, dan ragam
1. Rumus Rataan Hitung (Mean)
Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebut mean.
Rata-rata hitung dihitung dengan cara membagi jumlah nilai data dengan banyaknya data. Rata-rata hitung bisa juga disebut mean.
a) Rumus Rataan Hitung dari Data Tunggal
b) Rumus Rataan Hitung Untuk Data yang Disajikan Dalam Distribusi Frekuensi
Dengan : fixi = frekuensi untuk nilai xi yang bersesuaian
xi = data ke-i
c) Rumus Rataan Hitung Gabungan
Contoh soal :
1.) Seorang peneliti mencatat banyak bayi yang lahir selama setahun di 20 kecamatan. Hasil pencatatannya disajikan berikut.
136 140 220 193 130 158 242 127 184 213
200 131 111 160 217 281 242 242 281 192
Hitunglah rataan hitung (mean) data tersebut.
Penyelesaian :
Perhatikan data berikut.
nilai ujian
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
frekuensi
|
3
|
5
|
12
|
17
|
14
|
6
|
3
|
2.) Seorang siswa dinyatakan lulus jika nilai ujiannya lebih tinggi dari nilai rata-rata dikurangi 1. Dari data di atas, yang lulus adalah :
Siswa dinyatakan lulus jika nilainya lebih dari :
6,07 – 1 = 5,07.
Jadi, jumlah yang lulus adalah :
= 17 + 14 + 6 + 3 = 40 orang.
a. Data yang belum dikelompokkan
Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus dilambangkan mo.
b. Data yang telah dikelompokkan
b. Data yang telah dikelompokkan
Rumus Modus dari data yang telah dikelompokkan dihitung dengan rumus:
Dengan : Mo = Modus
L = Tepi bawah kelas yang memiliki frekuensi tertinggi (kelas modus) i = Interval kelas
b1 = Frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sebelumnya
b2 = frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sesudahnya
Contoh soal :
1.)Tentukan modus dari data berikut ini.
a. 45, 50, 50, 64, 69, 70, 70, 70, 75, 80
b. 50, 65, 65, 66, 68, 73, 73, 90
c. 35, 42, 48, 50, 52, 55, 60
Pembahasan :
a. Oleh karena nilai 70 muncul paling banyak (yaitu tiga kali muncul), modusnya adalah 70.
b. Oleh karena nilai 65 dan 73 muncul paling banyak (yaitu dua kali muncul), modusnya adalah 65 dan 73 (tidak tunggal).
c. Data 35, 42, 48, 50, 52, 55, 60 tidak mempunyai modus
2.)Tabel 3. menunjukkan hasil ulangan matematika dari 71 siswa Kelas XI SMA Bhinneka. Tentukan modus dari data tersebut.
Interval Kelas
|
Frekuensi
|
40 – 44
|
2
|
45 – 49
|
2
|
50 – 54
|
6
|
55 – 59
|
8
|
60 – 64
|
10
|
65 – 69
|
11
|
75 – 79
|
6
|
80 – 84
|
4
|
85 – 89
|
4
|
90 – 94
|
3
|
Oleh karena kelas ke-7 mempunyai frekuensi terbesar (frekuensinya 15) maka kelas ke-7 merupakan kelas modus.
i = 44,5 – 39,5 = 5
L = Batas bawah nyata kelas ke-7 = 69,5 (tepi bawah kelas)
d1 = 15 – 11 = 4
d2 = 15 – 6 = 9
a) Data yang belum dikelompokkan
Untuk mencari median, data harus dikelompokan terlebih dahulu dari yang terkecil sampai yang terbesar.
b) Data yang Dikelompokkan
Contoh soal
Dengan : Qj = Kuartil ke-j
j = 1, 2, 3
i = Interval kelas
Lj = Tepi bawah kelas Qj
fk = Frekuensi kumulatif sebelum kelas Qj
f = Frekuensi kelas Qj
n = Banyak data
1.)Tentukan median, kuartil bawah, dan kuartil atas dari data berikut.
67
|
86
|
77
|
92
|
75
|
70
|
63
|
79
|
89
|
72
|
83
|
74
|
75
|
103
|
81
|
95
|
72
|
63
|
66
|
78
|
88
|
87
|
85
|
67
|
72
|
96
|
78
|
93
|
82
|
71
|
Urutkan data dari kecil ke besar hasilnya sebagai berikut.
No. Unit Data (xi)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Nilai Data
|
63
|
63
|
66
|
67
|
67
|
70
|
71
|
72
|
72
|
72
|
No. Unit Data (xi)
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
Nilai Data
|
74
|
75
|
75
|
77
|
78
|
78
|
79
|
81
|
82
|
83
|
No. Unit Data (xi)
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
Nilai Data
|
85
|
86
|
87
|
88
|
89
|
92
|
93
|
95
|
96
|
103
|
2.)Tentukan median, kuartil bawah, dan kuartil atas dari data pada Tabel. 4.
Interval Kelas
|
Frekuensi
|
40 – 44
|
2
|
45 – 49
|
2
|
50 – 54
|
6
|
55 – 59
|
8
|
60 – 64
|
10
|
65 – 69
|
11
|
70 – 74
|
15
|
75 – 79
|
6
|
80 – 84
|
4
|
85 – 89
|
4
|
90 – 94
|
3
|
Kunci Jawaban :
Kelas Interval
|
Frekuensi
|
Frekuensi Kumulatif
| |
40 – 44
|
2
|
2
| |
45 – 49
|
2
|
4
| |
50 – 54
|
6
|
10
| |
Q1 →
|
55 – 59
|
8
|
18
|
60 – 64
|
10
|
28
| |
Q2 →
|
65 – 69
|
11
|
39
|
Q3 →
|
70 – 74
|
15
|
54
|
75 – 79
|
6
|
60
| |
80 – 84
|
4
|
64
| |
85 – 89
|
4
|
68
| |
90 – 94
|
3
|
71
|
Jadi, kelas Q3 ada di kelas ke-7 (kelas 70 – 74)
4. Rumus Jangkauan ( J )
Selisih antara nilai data terbesar dengan nilai data terkecil.
1.)Tentukan Jangkauan!
Interval Kelas
|
Frekuensi
|
40 – 44
|
2
|
45 – 49
|
2
|
50 – 54
|
6
|
55 – 59
|
8
|
60 – 64
|
10
|
65 – 69
|
11
|
70 – 74
|
15
|
75 – 79
|
6
|
80 – 84
|
4
|
85 – 89
|
4
|
90 – 94
|
3
|
Penyelesaian :
Xmax = 92
Xmin = 42
92-42 = 50
5. Rumus Simpangan Quartil
Contoh Soal :
1.) Tentukan jangkauan interkuartil dan simpangan kuartil dari data berikut.
20 35 50 45 30 30 25 40 45 30 35
Penyelesaian:
Ingat hal pertama yang Anda lakukan adalah mengurutkan data tersebut untuk mencari kuartil atas dan kuartil bawahnya, yakni sebagai berikut.
Jadi, kuartil bawah (Q1) dan kuartil atas (Q3) dari data tersebut yakni 30 dan
QR = Q3 – Q1
QR = 45 – 30
QR = 15
Sedangkan simpangan kuartilnya yakni:
Qd = ½QR
Qd = ½.15
Qd = 7,5
Jadi, jangkauan interkuartil dan simpangan kuartil dari data tersebut adalah 15 dan 7,5.
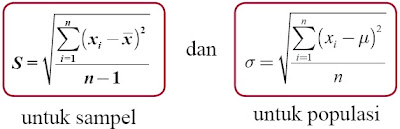
Diketahui sekumpulan data kuantitatif yang tidak dikelompokkan dan dinyatakan oleh x1, x2, …, xn. Dari data tersebut, dapat diperoleh nilai simpangan baku (S) yang ditentukan oleh rumus berikut.
Contoh Soal 1 :
Dari 40 orang siswa diambil sampel 9 orang untuk diukur tinggi badannya, diperoleh data berikut:
165, 170, 169, 168, 156, 160, 175, 162, 169.
Hitunglah simpangan baku sampel dari data tersebut.
Kunci Jawaban :
Jadi, simpangan bakunya adalah 5,83.
Sekumpulan data kuantitatif yang dikelompokkan, dapat dinyatakan oleh x1, x2, …, xn dan masing-masing data mempunyai frekuensi f1, f2, …, fn. Simpangan baku (S) dari data tersebut diperoleh dengan menggunakan rumus :
Contoh Soal 2 :
Hitunglah simpangan baku dari nilai ulangan Fisika dari 71 siswa kelas XI SMA Merdeka sesuai Tabel 1.
Jawaban :
Dari hasil perhitungan sebelumnya diperoleh µ = 65,7.
xi
|
fi
|
xi - µ
|
(xi - µ)2
|
Σfi (xi - µ)2
|
42
|
3
|
–23,7
|
561,69
|
1.685,07
|
47
|
4
|
–18,7
|
349,69
|
1.398,76
|
52
|
6
|
–13,7
|
187,69
|
1.126,14
|
57
|
8
|
– 8,7
|
75,69
|
605,52
|
62
|
10
|
–3,7
|
13,69
|
136,9
|
67
|
11
|
1,3
|
1,69
|
18,59
|
72
|
15
|
6,3
|
39,69
|
595,35
|
77
|
6
|
11,3
|
127,69
|
766,14
|
82
|
4
|
16,3
|
265,69
|
1.062,76
|
87
|
2
|
21,3
|
453,69
|
907,38
|
92
|
2
|
26,3
|
691,69
|
1.383,38
|
Σfi = 60
|
Σfi (xi - µ)2 = 9.685,99
|
Jadi, simpangan bakunya σ :
Contoh Soal 1 :
Hitung simpangan rata-rata dari data kuantitatif berikut :
12, 3, 11, 3, 4, 7, 5, 11
Pembahasan :
Jadi, simpangan rata-ratanya adalah 3,25.
Coba Anda tentukan simpangan rata-rata tersebut dengan menggunakan kalkulator. Apakah hasilnya sama?
Untuk sekumpulan data yang dinyatakan oleh x1, x2, …, xn dan masing-masing nilai data tersebut mempunyai frekuensi f1 , f2 , …, fn diperoleh nilai simpangan rata-rata (SR) dengan menggunakan rumus:
Contoh Soal 2 :
Hitunglah simpangan rata-rata nilai ulangan Fisika dari siswa Kelas XI SMA Merdeka seperti Tabel 1.
Tabel 1. Nilai ulangan Fisika dari siswa Kelas XI SMA Merdeka
Interval Kelas
|
Frekuensi
|
40 – 44
|
3
|
45 – 49
|
4
|
50 – 54
|
6
|
55 – 59
|
8
|
60 – 64
|
10
|
65 – 69
|
11
|
70 – 74
|
15
|
75 – 79
|
6
|
80 – 84
|
4
|
85 – 89
|
2
|
90 – 94
|
2
|
Penyelesaian :
Kelas
Interval
|
Nilai Tengah (xi)
|
fi
| ||
40 – 44
|
42
|
3
|
23,7
|
71,1
|
45 – 49
|
47
|
4
|
18,7
|
74,8
|
50 – 54
|
52
|
6
|
13,7
|
82,2
|
55 – 59
|
57
|
8
|
8,7
|
69,6
|
60 – 64
|
62
|
10
|
3,7
|
37
|
65 – 69
|
67
|
11
|
1,3
|
14,3
|
70 – 74
|
72
|
15
|
6,3
|
94,5
|
75 – 79
|
77
|
6
|
11,3
|
67,8
|
80 – 84
|
82
|
4
|
16,3
|
65,2
|
85 – 89
|
87
|
2
|
21,3
|
42,6
|
90 – 94
|
92
|
2
|
26,3
|
52,6
|
Σfi = 71
|
Jadi, simpangan rata-rata (SR) = 671,7 / 71 = 9,46.
Contoh soal :
1.) Dari 40 orang siswa diambil sampel 9 orang untuk diukur tinggi badannya, diperoleh data berikut:
165, 170, 169, 168, 156, 160, 175, 162, 169.
Hitunglah simpangan baku sampel dari data tersebut.
Kunci Jawaban :
v = S2 = (5,83)2 = 33,99.

























sangat membantu. terima kasih
ReplyDeleteSoal yang untuk modus apa tidak salah? Kok bisaa frekuensi 15?pdahal tertulis 6 mohon bantuan nya
ReplyDeleteHmmm iya ad yg slh aku jg pikir gitu soalnya
DeleteTerbuka diskusi untuk statistik terapan yang bermanfaat untuk penelitian ilmiah, silahkan kunjungi website Riads Solution Statistics Research & Information Technology Consulting | www.riadsolution.com
ReplyDeletekayaknya ada yang salah tapi sangat membantu saya
ReplyDeletethank's
makasih, mudah dimengerti
ReplyDeletesoal modus, kayaknya ada yang keliru di tabelnya deh. tolong direvisi kak biar gak dosa jariyah hehehe...
ReplyDeletebagus ka, saran aja sih bentuk soalnya agar bisa dibuat lebih beragam lagi
ReplyDeleteSangat membantu tapi tolong beri penjelasan lebih rinci lagi dan perbanyak contoh soal agar pembaca bisa memahami materi dengan baik.. 😄
ReplyDeleteIZIN COPY ADMIN
ReplyDeleteGak nyangka Sudah 4 Tahun Berlalu, Selamat datang Di 2020
ReplyDeleteFollow Ig:@dafa.satria_
nyatet bro:v
ReplyDelete