Turunan
Misalkan y adalah fungsi dari x atau y = f(x). Turunan (atau diferensial) dari y terhadap x dinotasikan dengan :

Rumus Turunan dan contoh
Jika
 dengan C dan n konstanta real, maka :
dengan C dan n konstanta real, maka : 
Jika y = C dengan

Jika y = f(x) + g(x) maka

Jika y = f(x).g(x) maka



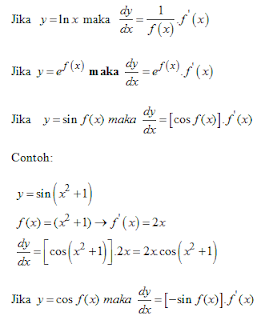


Contoh Soal :
- Tentukan turunan pertama dari y = sin 4x + cos 6x.
Pembahasan :
y' = 4 cos 4x − 6 sin 6x.y' = dy = d (sin 4x + cos 6x) dx dx - Tentukan turunan pertama dari y = 6 sin 2x − 4 cos x.
Pembahasan :
y' = 12 cos 2x − (-4 sin x)y' = dy = d (6 sin 2x − 4 cos x) dx dx
y' = 12 cos 2x + 4 sin x
- Jika y = 3x4 + sin 2x + cos 3x, maka tentukan turunan pertamanya.
Pembahasan :
y' = 12 x3 + 2 cos 2x − 3 sin 3x.y' = dy = d (3x4 + sin 2x + cos 3x) dx dx - Jika f(x) = sin x cos 3x, maka tentukan f '(π⁄6).
Pembahasan :
Kita dapat gunakan konsep turunan perkalian fungsi. Misalkan :
⇒ u(x) = sin x, maka u'(x) = cos x
⇒ v(x) = cos 3x, maka v'(x) = -3 sin 3x.
Maka turunan pertamanya adalah :
f '(x) = cos x (cos 3x) + sin x (-3 sin 3x)f '(x) = dy = u'(x).v(x) + u(x).v'(x) dx
f '(x) = cos x. cos 3x − 3 sin x. sin 3x
f '(π⁄6) = cos (π⁄6). cos 3(π⁄6) − 3 sin (π⁄6). sin 3(π⁄6)
f '(π⁄6) = {½√3 (0)} − {3 (½) (1)}
f '(π⁄6) = 0 − 3⁄2
f '(π⁄6) = -3⁄2 - Tentukan turunan pertama dari fungsi berikut :
y = 1 + cos x sin x
Pembahasan :
Kita dapat gunakan konsep turunan perkalian fungsi. Misalkan :
⇒ u(x) = 1 + cos x, maka u'(x) = -sin x
⇒ v(x) = sin x, maka v'(x) = cos x.
Maka turunan pertamanya adalah :
y' = dy = u'(x).v(x) − u(x).v'(x) dx v2(x) y' = -sin x (sin x) − (1 + cos x) (cos x) sin2 x y' = -sin2 x − cos2 x − cos x sin2 x y' = -(sin2 x + cos2 x) − cos x sin2 x y' = -(1) − cos x 1 − cos2 x y' = - (1 + cos x)(1 − cos x). (1 + cos x)y' = -1 1 − cos x y' = 1 cos x − 1
Turunan Kedua
Turunan kedua y = f(x) terhadap x dinotasikan dengan  . Turunan kedua diperoleh dengan menurunkan turunan pertama.
. Turunan kedua diperoleh dengan menurunkan turunan pertama.Contoh :
Sifat Sifat Turunan
Dalam mencari turunan, seringkali kita menjumpai dua fungsi atau lebih yang dijumlahkan, dikurangkan, dikalikan dan dibagikan. Untuk memudahkan perhitungan ini, dibuatlah sifat-sifat turunan.
Jika u dan v adalah fungsi dalam x, dan c adalah konstanta, maka berlaku
1. f(x) = u + v maka f '(x) = u' + v'
2. f(x) = u - v maka f '(x) = u'-v'
3. f(x) = c.u maka f '(x)=c.u'
4. f(x) = u.v maka f'(x) = u'v + uv'
5.
Bukti :
Sifat 1
f(x) = u(x) + v(x)
f '(x) = u'(x) + v'(x)
Sifat 2 :
f(x) = u(x) - v(x)
f '(x) = u'(x) - v'(x)
Sifat 3 :
f(x) = c.u(x) maka f '(x)=c.u'(x)
f '(x)=c.u'(x)
Sifat 4 :
f(x) = u(x).v(x) maka f'(x) = u'(x)v(x) + u(x)v'(x)
Sifat 5
Karena
maka
sehingga
Jika pembilang dan penyebut dikalikan dengan v(x) maka diperoleh
Contoh Soal :
- Jika f(x) = (2x – 1)2 (x + 2), maka f‘(x) = …A. 4(2x – 1)(x + 3)B. 2(2x – 1)(5x + 6)C. (2x – 1)(6x + 5)D. (2x – 1)(6x + 11)E. (2x – 1)(6x + 7)PEMBAHASAN :INGAT : f(x) = u.vf'(x) = u’v + uv’misal : u(x) = (2x – 1)2
u'(x) = 2(2x – 1)(2)
v(x) = x + 2v'(x) = 1
f'(x) = (4(2x – 1))(x + 2) + ((2x – 1)2)(1)= (8x – 4)(x + 2) + (2x – 1)2= 8x2 + 12x – 8 + 4x2 – 4x + 1= 12x2 + 8x – 7= (2x – 1)(6x + 7)JAWABAN : E - Turunan pertama dari fungsi f yang dinyatakan dengan f(x) =
adalah f ‘(x), maka f‘(x) = …
A.B.C.D.E.PEMBAHASAN :====JAWABAN : A - Diketahui f(x) =
, Jika f‘(x) adalah turunan pertama dari f(x), maka nilai f‘(2) = …
A. 0,1B. 1,6C. 2,5D. 5,0E. 7,0PEMBAHASAN :f(x) == (4x2+9)1/2f'(x) = 1/2 (4x2+9)-1/2 (8x)= 4x (4x2+9)-1/2=f'(2) === 1.6JAWABAN : B - Diketahui f(x) =
. Nilai f‘(4) = …
A. 1/3B. 3/7C. 3/5D. 1E. 4PEMBAHASAN :f(x) =f'(x) =misal : u(x) = 2x + 4u'(x) = 2
v(x) = 1 +v'(x) = 1/2 x-1/2
f'(x) =f'(4) ======
Persamaan Garis Singgung Kurva
Sebelum kita belajar ke materi inti yaitu cara mencari persamaan garis singgung kurva, kita harus tahu dulu mengenai gradien garis yang disimbolkan dengan m, dimana :
- gradian garis untuk persamaan y=mx+c adalah m
- gradien garis untuk persamaan ax+by=c, maka m=-a/b
- gradien garis jika diketahui dua titik, misal (x1,y1) dan (x2,y2) maka untuk mencari gradien garisnya m=(y2-y1)/(x2-x1)
Gradien dua garis lurus, berlaku ketentuan :
- jika saling sejajar maka m1=m2
- jika saling tegak lurus maka m1.m2=-1 atau m1=-1/(m2)
Persamaan Garis Singgung Kurva
Jika terdapat kurva y = f(x) disinggung oleh sebuah garis di titik (x1, y1) maka gradien garis singgung tersebut bisa dinyatakan dengan m = f'(x1). Sementara itu x1 dan y1 memiliki hubungan y1 = f(x1). Sehingga persamaan garis singgungnya bisa dinyatakan dengan y – y1 = m(x – x1).
Jadi intinya jika kita akan mencari persamaan garis singgung suatu kurva jika diketahui gradiennya m dan menyinggung di titik (x1,y1) maka kita gunakan persamaan
y-y1=m(x-x1)
Sedangkan jika diketahui 2 titik, misalnya (x1,y1) dan (x2,y2) maka untuk mencari persamaan garis singgung dari dua titik tersebut kita dapat gunakan persamaan
Contoh soal :
- Luas sebuah kotak tanpa tutup yang alasnya persegi adalah 432 cm2. Agar volume kotak tersebut mencapai maksimum, maka panjang rusuk persegi adalah … cm.A. 6B. 8C. 10D. 12E. 16PEMBAHASAN :misal kita anggap tinggi kotak adalah t dan panjang sisi alas adalah s.Luas kotak tanpa tutup = Luas alas (persegi) + (4 x luas sisi)432 = s2 + (4.s.t)432 = s2 + 4tsKarena yang diminta dalam soal adalah panjang sisi persegi, maka kita buat persamaan dalam variable s.432 – s2 = 4ts108/s – s/4 = tVolume = v(x) = s2t= s2(108/s – s/4)= 108s – s3/4Agar volume kotak maksimum maka :v'(x) = 0108 – 3s2/4 = 0108 = 3s2/4144 = s212 = sJAWABAN : D
2. Tentukan persamaan garis singgung pada kurva y = x³ – 3x di titik (2, 3) ?
Jawab :
f(x) = x³ – 3x
f ‘(x) = 3x² – 3
m = f ‘(2) = 12 – 3 = 9
f(x) = x³ – 3x
f ‘(x) = 3x² – 3
m = f ‘(2) = 12 – 3 = 9
Jadi, persamaan garis singgungnya adalah
y – y1 = m(x – x1)
y – 3 = 9 (x – 2)
y – 3 = 9x – 18
y = 9x – 15
y – y1 = m(x – x1)
y – 3 = 9 (x – 2)
y – 3 = 9x – 18
y = 9x – 15
3. Tentukan persamaan garis singgung pada kurva y = x4 – 7x2 + 20 di titik yang berabsis 2 ?
Jawab :
x = 2
y = x4 – 7x2 + 20 = y = 24 – 7.22 + 20 = 16 – 28 + 20 = 8
m =y’ = 4x3 – 14 x = 4.23 – 14.2 = 32 – 28 = 4
x = 2
y = x4 – 7x2 + 20 = y = 24 – 7.22 + 20 = 16 – 28 + 20 = 8
m =y’ = 4x3 – 14 x = 4.23 – 14.2 = 32 – 28 = 4
Jadi, persamaan garis singgungnya adalah
y – y1 = m(x – x1)
y – 8 = 4(x – 2)
y – 8 = 4x – 8
y = 4x
y – y1 = m(x – x1)
y – 8 = 4(x – 2)
y – 8 = 4x – 8
y = 4x
4. Tentukan persamaan garis singgung pada kurva y = x3 + 10 di titik yang berordinat 18 ?
Jawab :
Ordinat adalah nilai y, maka
y = 18
x3 + 10 = 18
x3 = 8
x = 2
Ordinat adalah nilai y, maka
y = 18
x3 + 10 = 18
x3 = 8
x = 2
m = y’ = 3x2 = 3.22 = 12
Sehingga persamaan garis singgungnya
y – y1 = m(x – x1)
y – 18 = 12(x – 2)
y – 8 = 12x – 24
y = 12x – 16
y – y1 = m(x – x1)
y – 18 = 12(x – 2)
y – 8 = 12x – 24
y = 12x – 16
5. Persamaan garis singgung pada kurva y = x4 – 5x2 + 10 di titik yang berordinat 6 adalah
Jawab :
ordinat = 6
x4 – 5x2 + 10 = 6
x4 – 5x2 + 4 = 0
(x2 – 1)(x2 – 4) = 0
(x + 1)(x – 1)(x + 2)(x – 2) = 0
x = -1 atau x = 1 atau x = -2 atu x = 2
ordinat = 6
x4 – 5x2 + 10 = 6
x4 – 5x2 + 4 = 0
(x2 – 1)(x2 – 4) = 0
(x + 1)(x – 1)(x + 2)(x – 2) = 0
x = -1 atau x = 1 atau x = -2 atu x = 2
untuk x = -1
m = 4x3 – 10x = -4 + 10 = 6
y – y1 = m(x – x1)
y – 6 = 6(x + 1)
y – 6 = 6x + 6
y = 6x + 12
m = 4x3 – 10x = -4 + 10 = 6
y – y1 = m(x – x1)
y – 6 = 6(x + 1)
y – 6 = 6x + 6
y = 6x + 12
Untuk x = 1
m = 4x3 – 10x = 4 – 10 = -6
y – y1 = m(x – x1)
y – 6 = -6(x – 1)
y – 6 = -6x + 6
y = -6x + 12
m = 4x3 – 10x = 4 – 10 = -6
y – y1 = m(x – x1)
y – 6 = -6(x – 1)
y – 6 = -6x + 6
y = -6x + 12
Untuk x = -2
m = 4x3 – 10x = 4(-2)3 – 10(-2) = 4(-8) + 20 = -32 + 20 = -12
y – y1 = m(x – x1)
y – 6 = -12(x + 2)
y – 6 = -12x – 24
y = -12x – 18
m = 4x3 – 10x = 4(-2)3 – 10(-2) = 4(-8) + 20 = -32 + 20 = -12
y – y1 = m(x – x1)
y – 6 = -12(x + 2)
y – 6 = -12x – 24
y = -12x – 18
Untuk x = 2
m = 4x3 – 10x = 4.23 – 10.2 = 4.8 – 20 = 32 – 20 = 12
y – y1 = m(x – x1)
y – 6 = 12(x – 2)
y – 6 = 12x – 24
y = 12x – 18
m = 4x3 – 10x = 4.23 – 10.2 = 4.8 – 20 = 32 – 20 = 12
y – y1 = m(x – x1)
y – 6 = 12(x – 2)
y – 6 = 12x – 24
y = 12x – 18
Jadi, ada 4 persamaan garis singung, yaitu y = 6x + 12, y = -6x = 12, y = -12x – 18 dan y = 12x – 18
6. Persamaan garis singgung pada kurva y = 3x4 – 20 yang sejajar dengan garis y = 12x + 8 adalah
Jawab :
y = 3x4 – 20
y’ = 12x3
Persamaan garis yang sejajar dengan garis singgung adalah
y = 12x + 8
maka gradien garis ini adalah m1 = 12
Karena sejajar maka gradiennya sama sehingga gradien garis singgung (m2) adalah
m2 = m1 = 12
gradien garis singgung ini sama dengan turunan kurva sehingga
y’ = 12
12x3 = 12
x3 = 1
x = 1
maka y = 3x4 – 20 = 3 – 20 = – 17
Persamaan garis singgungnya adalah
y – y1 = m(x – x1)
y + 17 = 12(x – 1)
y + 17 = 12x – 12
y = 12x – 29
y = 3x4 – 20
y’ = 12x3
Persamaan garis yang sejajar dengan garis singgung adalah
y = 12x + 8
maka gradien garis ini adalah m1 = 12
Karena sejajar maka gradiennya sama sehingga gradien garis singgung (m2) adalah
m2 = m1 = 12
gradien garis singgung ini sama dengan turunan kurva sehingga
y’ = 12
12x3 = 12
x3 = 1
x = 1
maka y = 3x4 – 20 = 3 – 20 = – 17
Persamaan garis singgungnya adalah
y – y1 = m(x – x1)
y + 17 = 12(x – 1)
y + 17 = 12x – 12
y = 12x – 29
7. Garis yang menyinggung kurva y = 12 – x4 dan tegak lurus dengan x – 32y = 48 mempunyai persamaan ….
Jawab :
y = 12 – x4
y’ = – 4x3
y = 12 – x4
y’ = – 4x3
Sedangkan
x – 32y = 48
32y = x – 48
x – 32y = 48
32y = x – 48
Garis ini memiliki gradien m1=1/32
Karena garis singgungnya tegak lurus dengan garis ini maka
Karena garis singgungnya tegak lurus dengan garis ini maka
m1.m2 = -1
(1/32)m2=-1
m2= -32
m2 ini adalah gradien garis singgung, sehingga sama dengan turunan
y’ = -32
– 4x3 = -32
x3 = 8
x = 2
y = 12 – x4 = 12-24 = -4
maka persamaan garis singgungnya
y – y1 = m(x – x1)
y + 4 = -32(x – 2)
y + 4 = -32x + 64
y = -32x + 60
(1/32)m2=-1
m2= -32
m2 ini adalah gradien garis singgung, sehingga sama dengan turunan
y’ = -32
– 4x3 = -32
x3 = 8
x = 2
y = 12 – x4 = 12-24 = -4
maka persamaan garis singgungnya
y – y1 = m(x – x1)
y + 4 = -32(x – 2)
y + 4 = -32x + 64
y = -32x + 60
Tentunya kalian masih ingat dengan topik sebelumnya tentang menentukan titik maksimum, titik minimum, dan titik belok. Pada topik ini, kalian akan belajar tentang penggunaan turunan dalam menentukan nilai maksimum dan nilai minimum.
Definisi 1 :
Jika diberikan fungsi f dengan daerah asal Df dan x = c merupakan anggota Df, maka berlaku hubungan sebagai berkut :
- f(c) adalah nilai maksimum fungsi f pada Df jika f(c) ≥ f(x) untuk semua x di Df
- f(c) adalah nilai minimum fungsi f pada Df jika f(c) ≤ f(x) untuk semua x di Df
- f(c) adalah nilai ekstrim fungsi f pada Df jika f(c) adalah nilai maksimum atau minimum fungsi f di Df
Definisi 2 :
Jika diberikan fungsi f dengan daerah asal Df dan interval (a,b) merupakan himpunan bagian dari Df, maka berlaku hubungan sebagai berkut :
- f(c) adalah nilai maksimum lokal fungsi f pada interval (a,b) yang memuat c jika f(c)adalah nilai maksimum fungsi f pada (a,b)
- f(c) adalah nilai minimum lokal fungsi f pada interval (a,b) yang memuat c jika f(c)adalah nilai minimum fungsi f pada (a,b)
- f(c) adalah nilai ekstrim lokal fungsi f jika f(c) adalah nilai maksimum lokal atau nilai minimum lokal fungsi f[/important
Lalu, kapan terjadi nilai ekstrim lokal?
Kalian dapat menggunakan uji turunan pertama untuk menentukan nilai ekstrim lokal.
Jika fungsi f kontinu pada selang terbuka (a,b) yang memuat x = c, maka berlaku hubungan sebagai berikut :
- Jika f'(x) > 0 untuk semua nilai x dalam selang (a,c) dan f'(x) < 0 untuk semua nilai x dalam selang (c,b), maka f(c) merupakan nilai maksimum lokal f
- Jika f'(x) < 0 untuk semua nilai x dalam selang (a,c) dan f'(x) > 0 untuk semua nilai x dalam selang (c,b), maka f(c) merupakan nilai minimum lokal f
- Jika f'(x) pada selang (a,c) dan (c,b), maka f(c) bukan merupakan nilai ekstrim lokal f
Agar lebih jelas, mari perhatikan gambar di bawah ini.
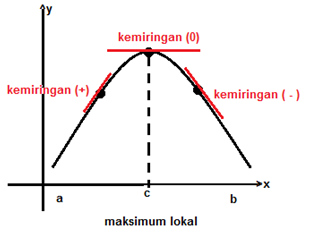
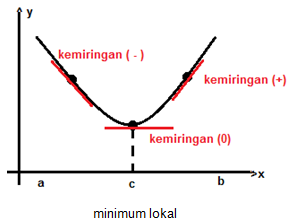
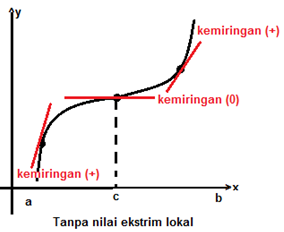
Apakah kalian sudah paham? Mari kita cermati beberapa contoh berikut ini.
Contoh 1:
Tentukan nilai maksimum dan minimum dari f(x) = 2x2 - x jika Df = { x | -1 ≤ x ≤ 2} !
Penyelesaian :
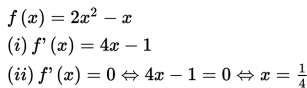
Jika kita perhatikan, ternyata x = ¼ merupakan anggota Df = { x | -1 ≤ x ≤ 2 }. Dengan demikian, untuk menentukan nilai maksimum dan nilai minimum fungsi f pada Df, kita perlu mengetahui nilai f untuk x = -1 , x = ¼, dan x = 2.
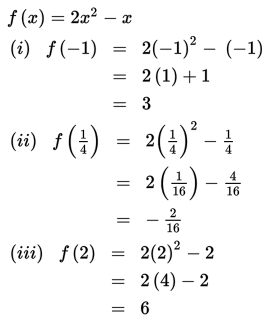
Berdasarkan uraian di atas, dapat disimpulkan bahwa nilai maksimum dan minimum dari
f(x) = 2x2 – x dengan Df = { x | -1 ≤ x ≤ 2 } berturut-turut adalah f(2) = 6 dan f( ¼ ) = - 1/8.
f(x) = 2x2 – x dengan Df = { x | -1 ≤ x ≤ 2 } berturut-turut adalah f(2) = 6 dan f( ¼ ) = - 1/8.
Contoh 2 :
Tentukan nilai maksimum dan minimum dari f(x) = 3x2 - 2x + 1 jika Df = { x | 1 ≤ x ≤ 4 } !
Penyelesaian :

Oleh karena x = 1/3 bukan merupakan anggota Df = { x | 1 ≤ x ≤ 4 }, maka untuk menentukan nilai minimum dan nilai maksimum untuk fungsi f, kita cukup mengetahui nilai f untuk x = 1 dan x = 4.
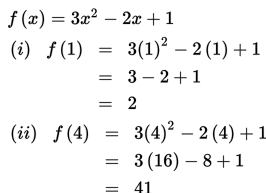
Berdasarkan uraian di atas, dapat disimpulkan bahwa nilai maksimum dan minimum dari
f(x) = 3x2 – 2x + 1 dengan Df = { x | 1 ≤ x ≤ 4 } berturut-turut adalah f(4) = 41 dan f(1) = 2.
f(x) = 3x2 – 2x + 1 dengan Df = { x | 1 ≤ x ≤ 4 } berturut-turut adalah f(4) = 41 dan f(1) = 2.
Contoh 3 :
Tentukan nilai maksimum dan minimum dari f(x) = (x + 4)2 jika Df = { x | -4 ≤ x ≤ 0 } !
Penyelesaian :
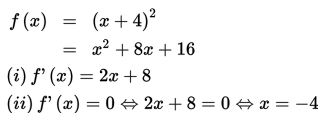
Oleh karena x = -4 merupakan batas kiri dari Df = { x | -4 ≤ x ≤ 0 }, maka untuk menentukan nilai minimum dan nilai maksimum untuk fungsi f, kita cukup mengetahui nilai f untuk x = -4 dan x = 0.
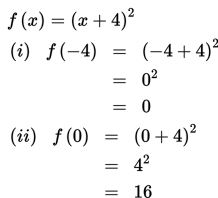
Berdasarkan uraian di atas, dapat disimpulkan bahwa nilai maksimum dan minimum dari
f(x) = (x + 4)2 dengan Df = { x | -4 ≤ x ≤ 0 } berturut-turut adalah f(0) = 16 dan f(-4) = 0.
f(x) = (x + 4)2 dengan Df = { x | -4 ≤ x ≤ 0 } berturut-turut adalah f(0) = 16 dan f(-4) = 0.




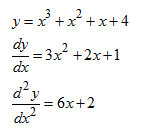


Ini sangat membantu....
ReplyDeleteTerimakasi atas materinya.
bagussss
ReplyDeleteapikk tenannn
Terima kasih ilmunya
ReplyDeleteperfect! izin copas, makasih...
ReplyDeleteterima kasih atas ilmunya... sangat membantu untuk belajar sendiri
ReplyDeleteTerimakasih. Lengkap bgt!
ReplyDeleteBagus banget kak kembangkan lagi ya
DeleteTerimakasih..
ReplyDeletekak mau tentukan interval fungsi naik daan fungsi turun dari x pangkat 3 ditambah 6 x pangkat 2 dikurangi 15 x ditambah 10
ReplyDeleteTerima kasih kak, lengkap banget materi nya. Mudah di pahami lagi😊
ReplyDeleteTerima kasih
ReplyDeleteSangat sangat membantu..terimakasih
ReplyDeleteterima kasih pencerahannya kakak, sehat selalu
ReplyDeleteTerima kasih kak
ReplyDeleteTerimakasih kak, artikel nya membantu sekali. Semangat buat artikel² lain lagi ya kak^^
ReplyDeleteTerimakasih banyak kak...
ReplyDelete