Materi Matematika Kelas XI Semester 2: Bab V Transformasi

TRANSFORMASI GEOMETRI

Transformasi merupakan suatu pemetaan titik pada suatu bidang ke himpunan titik pada bidang yang sama. Jenis-jenis dari transformasi yang dapat dilakukan antara lain :

Translasi (Pergeseran)
Refleksi(Pencerminan)
Rotasi(Perputaran)
Dilatasi(Penskalaan)

Berikut ini ilustrasinya :

TRANSLASI / PERGESERAN

Berdasarkan gambar di atas, segitiga ABC yang mempunyai koordinat A(3, 9), B(3, 3), C(6, 3) ditranslasikan:

Berdasarkan penjelasan diatas, maka untuk mencari nilai translasi dapat digunakan rumus sebagai berikut :

dimana :

a menyatakan pergeseran horizontal (kekanan+, kekiri-)
b menyatakan pergeseran vertikal (keatas+,kebawah-)

Contoh Soal :

Soal No. 1
a) Tentukan bayangan dari titik A (2, 3) oleh translasi T = (7, 8)

b) Tentukan bayangan dari

titik A (5, 10) oleh translasi

c) Tentukan bayangan dari titik A (1, 2) oleh translasi T = (1, 2) dilanjutkan oleh translasi U = (3, 4)

Pembahasan
Bayangan dari titik A oleh suatu transformasi namakan A’ Dua model yang biasa dipakai sebagai berikut:

Hasilnya akan sama saja, hanya sedikit beda cara penulisan, sehingga:

a) Bayangan dari titik A (2, 3) oleh translasi T = (7, 8)

b) Bayangan dari titik A (5, 10) oleh translasi

c) Bayangan dari titik A (1, 2) oleh translasi T = (1, 2) dilanjutkan oleh translasi U = (3, 4)

Soal No. 2
Disediakan suatu persamaan garis lurus
Y = 3x + 5
Tentukan persamaan garis lurus yang dihasilkan oleh translasi T = (2, 1)

Pembahasan
Ada beberapa cara diantaranya:
Cara pertama:
Posisi titik (x, y) oleh translasi T = (2, 1) adalah:
x’ = x + 2 → x = x’ – 2
y’ = y + 1 → y = y’ – 1

Masukkan nilai x dan y yang baru ke persamaan asal
y = 3x + 5
(y’ – 1 ) = 3(x’ – 2) + 5

Tinggal selesaikan, ubah lambang y’ dan x’ ke y dan x lagi:
y – 1 = 3x – 6 + 5
y = 3x – 6 + 5 + 1
y = 3x

Cara kedua:
Ambil dua buah titik dari persamaan y = 3x + 5
Misal:
Titik A, untuk x = 0 → y = 5 dapat titik A (0, 5)
Titik B, untuk Y = 0 → x = –⁵ /₃ dapat titik B (– ⁵/₃ , 0)

Translasikan Titik A dan B dengan T = (2,1)
A’ (0 + 2, 5 +1) = A’ (2, 6)
B’ (-5/3 + 2, 0 + 1) = A’ (1/3, 1)

Buat persamaan garis yang melalui kedua titik itu:

Cara ketiga
Dengan rumus yang sudah jadi atau rumus cepat:

ax + by = c
Translasi T (p, q)
Hasil :
ax + by = c + ap + bq

Rumus ini untuk bentuk seperti soal di atas, jangan terapkan pada bentuk-bentuk yang lain, nanti salah.
y = 3x + 5
atau
3x − y = − 5
oleh T = (2,1)

Hasil translasinya adalah:
3x − y = − 5 + (3)(2) + (− 1)(1)
3x − y = − 5 + 6 − 1
3x − y = 0
atau
y = 3x

REFLEKSI / PENCERMINAN

Segitiga ABC dengan koordinat A(3, 9), B(3, 3), C(6, 3) dicerminkan:

terhadap sumbu Y menjadi segitiga A2B2C2 dengan koordinat A2(-3, 9), B2(-3, 3), C2(-6, 3)
terhadap sumbu X menjadi segitiga A3B3C3 dengan koordinat A3(3, -9), B3(3, -3), C3(6, -3)
terhadap titik (0, 0) menjadi segitiga A4B4C4 dengan koordinat A4(-3, -9), B4(-3, -3), C4(-6, -3)

Segitiga ABC dengan koordinat A(3, 9), B(3, 3), C(6, 3) dicerminkan:

terhadap garis x = -2 menjadi segitiga A5B5C5 dengan koordinat A5(-7, 9), B5(-7, 3), C5(-10, 3)
terhadap sumbu y = 1 menjadi segitiga A6B6C6 dengan koordinat A6(3, -7), B6(3, -1), C6(6, -1)

Segitiga PQR dengan koordinat P(6, 4), Q(6, 1), R(10, 1) dicerminkan:

terhadap garis y = x menjadi segitiga P2Q2R2 dengan koordinat P2(4, 6), Q2(1, 6), R2(1, 10)
terhadap garis y = -x menjadi segitiga P3Q3R3 dengan koordinat P3(-4, -6), Q3(-1, -6), R3(-1, -10)

Berdasarkan penjelasan diatas dapat dirumuskan :

Pencerminan terhadap garis x = a atau y = b

Pencerminan terhadap sumbu x atau sumbu y

Pencerminan terhadap titik (0, 0)

Pencerminan terhadap garis y = x atau y = –x

Pencerminan terhadap garis y = mx + c

Jika m = tan θ maka:

Contoh Soal :

6.) Titik A memiliki koordinat (3, 5). Tentukan koordinat hasil pencerminan titik A:
a) Terhadap garis x = 10
b) Terhadap garis y = 8

Pembahasan
Pencerminan sebuah titik terhadap garis x = h atau y = k
a) Terhadap garis x = 10
           x = h
(a, b) ----------> (2h − a, b)

           x = h
(3, 5) ----------> ( 2(10) − 3, 5) = (17, 5)

b) Terhadap garis y = 8
           y = k
(a, b) ----------> (a, 2k − b)

            y = k
(3, 5) ----------> ( 3, 2(8) − 5) = (3, 11)

7.) Titik A memiliki koordinat (3, 5). Tentukan koordinat hasil pencerminan titik A:
a) Terhadap garis y = x
b) Terhadap garis y = − x

Pembahasan
a) Terhadap garis y = x
           y = x
(a, b) ----------> ( b, a)

           y = x
(3, 5) ----------> (5, 3)

b) Terhadap garis y = − x
           y = − x
(a, b) ----------> ( − b, − a)

            y = − x
(3, 5) ----------> (− 5, − 3)

ROTASI / PERPUTARAN

rotasi	matriks	perubahan titik	perubahan fungsi
½ p	é0 -1ù ë1 -0 û	(x,y) ® (-y,x)	F(x,y) = 0 ® F(y,-x) = 0
p	é-1 0ù ë1 -1 û	(x,y) ® (-x,-y)	F(x,y) = 0 ® F(-x,-y) = 0
3/2 p	é0 -1ù ë-1 0 û	(x,y) ® (y,-x)	F(x,y) = 0 ® F(-y,x) = 0
q	écosq -sinq ù ësinq cosq û	(x,y) ® (x cos q - y sinq, x sin q + y cos q) F(x,y) = 0 ® F(x cos q + y sin q, -x sin q + y cos q) = 0

Untuk rotasi searah jarum jam, sudut diberi tanda negatif (–)

Untuk rotasi berlawanan arah jarum jam, sudut diberi tanda positif (+)

Segitiga ABC dengan koordinat A(3, 9), B(3, 3), C(6, 3) dirotasi:

+90° atau –270° dengan pusat rotasi O(0, 0) menjadi segitiga A2B2C2 dengan koordinat A2(-9, 3), B2(-3, 3), C2(-3, 6)
+270° atau –90° dengan pusat rotasi O(0, 0) menjadi segitiga A3B3C3 dengan koordinat A2(9, -3), B2(3, -3), C2(3, -6)
+180° atau –180° dengan pusat rotasi O(0, 0) menjadi segitiga A4B4C4 dengan koordinat A4(-3, -9), B4(-3, -3), C4(-6, -3)

Berdasarkan penjelasan diatas, maka rotasi dapat dirumuskan sebagai berikut :

Rotasi sejauh θ dengan pusat (a, b)

Rumus praktis untuk rotasi dengan pusat rotasi O(0, 0):

Contoh Soal :

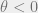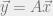1.) Vektor $\vec{x}$ diputar terhadap titik asal O sebesar $\theta < 0$ searah jarum jam. Kemudian hasilnya dicerminkan terhadap garis $y=-x$ , menghasilkan vektor $\vec{y}$ . Jika $\vec{y} = A\vec{x}$ , maka matriks $A$ = …

$\begin{bmatrix} \cos \theta & \sin \theta\\ -\sin\theta & \cos\theta\end{bmatrix} \begin{bmatrix} 0 & -1 \\-1 & 0\end{bmatrix}$
$\begin{bmatrix} 0 & -1 \\-1 & 0\end{bmatrix} \begin{bmatrix} \cos \theta & \sin \theta\\ -\sin\theta & \cos\theta\end{bmatrix}$
$\begin{bmatrix} \cos \theta & -\sin \theta\\ -\sin\theta & \cos\theta\end{bmatrix} \begin{bmatrix} 0 & -1 \\-1 & 0\end{bmatrix}$
$\begin{bmatrix} 0 & -1 \\1 & 0 \end{bmatrix} \begin{bmatrix} \cos \theta & \sin \theta\\ \sin\theta & -\cos\theta\end{bmatrix}$
$\begin{bmatrix} \cos \theta & \sin \theta\\ -\sin\theta & \cos\theta\end{bmatrix} \begin{bmatrix} 0 & 1 \\1 & 0 \end{bmatrix}$

Jawab :
Matriks tranformasi untuk rotasi dengan pusat rotasi (0, 0) dan sudut putar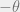 $-\theta$ (searah jarum jam

$\displaystyle \begin{aligned} M_1 = \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} \end{aligned}$

Matriks tranformasi untuk Refleksi terhadap $y=-x$

$\displaystyle \begin{aligned} M_1 = \begin{bmatrix} 0 & -1 \\ -1 & 0 \end{bmatrix} \end{aligned}$

$\vec{x}$ ditransformasi berturut-turut oleh $M_1$ dan $M_2$ menjadi $\vec{y}$ dengan hubungan $\vec{y} = A\vec{x}$ , sehingga $A$ adalah matriks komposisi dari $M_1$ dan $M_2$

$\displaystyle \begin{aligned} A &= M_2 \circ M_1 \\ &= \begin{bmatrix} 0 & -1 \\ -1 & 0 \end{bmatrix} \begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{bmatrix} \end{aligned}$

Jawaban : B

3.) Titik P (6√2, 10√2) diputar dengan arah berlawanan jarum jam sejauh 45° menghasilkan titik P'. Tentukan koordinat dari titik P'.

Pembahasan
Rotasi sebuah titik dengan sudut sebesar α

Sehingga:

Catatan:
sudut α positif → berlawanan arah jarum jam
sudut α negatif → searah jarum jam

DILATASI / PENSKALAAN

Segitiga ABC dengan koordinat A(3, 9), B(3, 3), C(6, 3) didilatasi:

dengan faktor skala k = 1/3 dan pusat dilatasi O(0, 0) menjadi segitiga A2B2C2 dengan koordinat A2(1, 3), B2(1, 1), C2(2, 1)
dengan faktor skala k = 2 dan pusat dilatasi O(0, 0) menjadi segitiga A3B3C3 dengan koordinat A3(6, 18), B3(6, 6), C3(12, 6)

Untuk nilai k negatif, arah bayangan berlawanan dengan arah aslinya.

Berdasarkan penjelasan diatas, maka dapat dirumuskan :

Dilatasi dengan pusat (a, b) dan faktor skala k

Rumus praktis dilatasi dengan faktor skala k dan pusat dilatasi O(0, 0):

Contoh soal:

1. Tentukan bayangan persegi panjang ABCD dengan

A(2,2) , B(-2,2) , C(-2,-2) dan D(2,-2)

jika dilakukan transformasi Dilatasi pusat O dan skala 3 adalah....

jawab :

$\fn_jvn \begin{bmatrix} 3 & 0\\ 0& 3 \end{bmatrix}.\begin{bmatrix} 2 & -2 & -2& 2\\ 2&2 & -2 & -2 \end{bmatrix}=\begin{bmatrix} 6& -6& -6& 6\\ 6&6 & -6 & -6 \end{bmatrix}$

Jadi hasilnya A'(6,6) , B'(-6,6) , C'(-6,-6) dan D'(6,-6)

2. Bayangan garis x - y - 3 = 0 oleh D(O,4) adalah.....

Jawab :

Transformasinya adalah Dilatasi dengan pusat O(0,0) dan skala 4

$\dpi{100} \fn_jvn x=\frac{x\, '}{4}\:\: dan\: \: y=\frac{y\, '}{4}$

$\dpi{100} \fn_jvn bayangannya\: \: \: \: \frac{x\, '}{4}-\frac{y\, '}{4}-3=0$

dengan menghilangkan  tanda aksen dan mengalikan dengan 4 maka 

bayangan / peta / hasilnya adalah  x - y - 12 = 0

Bagaimana jika mendilatasikan dengan pusat di suatu titik yang
bukan titik O(0,0) misal A(p,q) dan faktor skala k ....???
maka bentuk operasinya menjadi :

$\dpi{100} \fn_jvn \begin{bmatrix} k & 0\\ 0& k \end{bmatrix}.\begin{bmatrix} x{\color{Red} -p}\\ y{\color{Blue} -q} \end{bmatrix}+\begin{bmatrix} {\color{Red} p}\\ {\color{Blue} q} \end{bmatrix}=\begin{bmatrix} x\, '\\ y\, ' \end{bmatrix}$

atau dapat ditulis :

k.(x-p) = x' - p dan k.(y-q) = y' - q

3. Bayangan titik W(2,6) oleh dilatasi dengan pusat (2,-1) dan faktor

skala -2 adalah ......

Jawab :

-2(2-2) = x' - 2 maka x' = 2

-2(6+1) = y' +1 maka y' = - 15

jadi bayangannya W'(2,-15)

4. Bayangan garis y = x - 3 karena dilatasi faktor skala 4

dengan pusat A(1,2) adalah .....

Jawab :

$\dpi{100} \fn_jvn \begin{matrix} 4.(x-1)=x\, '-1\Rightarrow 4x-4=x'-1\\ 4.(y-2)=y\, \, '-2\Rightarrow 4y-8=y'-2 \end{matrix}$

atau dapat ditulis menjadi

$\fn_jvn \begin{matrix} x=\frac{x'+3}{4}\\ y=\frac{y'+6}{4} \end{matrix}$

sehingga bayangannya adalah :

$\dpi{100} \fn_jvn \frac{y\, '+6}{4}=\frac{x\, '+3}{4}-3\Rightarrow y'=x'+15$

atau ditulis y = x + 15 atau x - y + 15 = 0

Transformasi dengan Matriks Transformasi Tertentu

KOMPOSISI TRANSFORMASI

merupakan gabungan dari beberapa transformasi. Misalnya kita mempunyai transformasi T1 akan dilanjutkan ke T2 maka ditulis T2oT1.

Komposisi Khusus :

1. Dua pencerminan yang berurutan terhadap sumbu-sumbu yang sejajar

2. Dua pencerminan yang berurutan terhadap dua sumbu yang tegak lurus ekuivalen dengan rotasi 180º yang pusatnya adalah titik potong kedua sumbu tersebut.

3. Dua pencerminan terhadap dua sumbu yang berpotongan ekuivalen dengan rotasi dimana titik pusat adalah titik potong kedua sumbu dan sudutnya adalah sudut antara kedua sumbu.

4. Dua rotasi berurutan terhadap pusat yang sama ekuivalen dengan rotasi dimana pusatnya sejauh jumlah sudut keduanya.

LUAS HASIL TRANSFORMASI

Transformasi yang berupa translasi, refleksi, dan rotasi tidak mengubah luas suatu benda

Mencari luas segitiga ABC jika diketahui koordinat titik A, B, dan C nya, maka kita dapat gunakan rumus :

Perhatikan contoh soal transformasi berikut ini.

Tentukanlah persamaan bayangan kurva y = x2 + 3x -4 jika dicerminkan terhadap sumbu X, kemudian didilatasikan dengan faktor skala 2 dengan pusat dilatasi O(0, 0)

Penyelesaian :

cara 1 : cara langsung

cara 2 : menggunakan matriks

2.) Bayangan kurva y = x + 1 jika ditransformasikan oleh matriks

kemudian dilanjutkan oleh pencerminan terhadap sumbu X adalah....
A. x + y − 3 = 0
B. x − y − 3 = 0
C. x + y + 3 = 0
D. 3x + y + 1 = 0
E. x + 3y + 1 = 0
(UN Matematika Tahun 2010 P04)

Pembahasan

Transformasi oleh matriks

dilanjutkan pencerminan terhadap sumbu x dengan matriksnya

Gabungan dua transformasi:

Terlihat bahwa
y' = − y
y = − y'

x' = x + 2y
x' = x + 2(− y')
x' = x − 2y'
x = x' + 2y'

Jadi:
x = x' + 2y'
y = − y'

Masukkan ke persamaan awal
y = x + 1
(− y') = (x' + 2y' ) + 1
x' + 3y' + 1 = 0

Sehingga bayangan kurva yang diminta adalah x + 3y + 1 = 0

3.)Koordinat bayangan titik P(6, 5) jika ditransformasikan oleh matriks

dan dilanjutkan pencerminan terhadap sumbu X adalah....
A. (−11, 6)
B. (−6, 11)
C. (−5, 11)
D. (11, −5)
E. (11, −6)

Pembahasan
Titik A, dengan transformasi matriks

akan menghasilkan titik A', yang koordinatnya:

Dilanjutkan lagi dengan pencerminan terhadap sumbu X akan menghasilkan titik A'', dimana titik A'' koordinatnya akan menjadi (11, −6), beda tanda minus saja pada ordinat atau y nya. Bisa juga dengan mengalikan memakai matriks pencerminan terhadap sumbu X.

Jadi A" koordinatnya adalah (11, −6)

4.) Lingkaran (x − 2)² + (y + 3)² = 25 ditransformasikan oleh matriks

dilanjutkan oleh matriks

maka bayangan lingkaran itu adalah....
A. x² + y² + 6x − 4x − 12 = 0
B. x² + y² − 6x − 4x − 12 = 0
C. x² + y² − 4x − 6x − 12 = 0
D. x² + y² + 4x − 6x − 12 = 0
E. x² + y² + 4x + 6x − 12 = 0

Pembahasan
(x − 2)² + (y + 3)² = 25 adalah sebuah lingkaran yang berpusat di titik P (2, − 3) dan berjari-jari r = √25 = 5. Ingat kembali topik persamaaan lingkaran.

Setelah diitransformasi, jari-jarinya tidak berubah, tetap r = 5, jadi cukup dengan transformasi titik pusatnya, kemudian dipasang lagi di persamaan umum lingkaran akan diperoleh hasilnya.

Titik P (2, − 3) oleh transformasi

akan menjadi P':

Titik P' ini oleh transformasi kedua

akan menjadi P" dengan koordinatnya tetap (3, 2). Kok tidak berubah, karena matriks yang kedua ini adalah matriks identitas, jika untuk mengali hasilnya tetap. Atau dihitung sajalah seperti ini: